Análisis de circuitos por teoremas

4.- Teorema de Thévenin y Norton

Suponga que se necesita efectuar solo un análisis parcial de un circuito. Por ejemplo, quizás se requiera determinar la corriente, tensión y la potencia que se entregan a una resistencia de “carga” por medio del resto del circuito, el cual quizás consta de un número considerable de fuentes y resistencias (Figura 4.1a). O tal vez se desee determinar la respuesta para diferentes valores de la resistencia de carga. El teorema de Thévenin dice que se puede sustituir todo excepto la resistencia de carga, por una fuente de tensión independiente en serie con una resistencia (Figura 4.1b); la respuesta media de la resistencia de carga permanecerá invariable. Mediante el teorema de Norton, se obtiene un equivalente compuesto por una fuente de corriente independiente en paralelo con una resistencia (Figura 4.1c).

Figura 4.1.- a) Red compleja que incluye una resistencia de carga R_L. b) Red equivalente de Thévenin conectada a la resistencia de carga R_L. c) Red equivalente de Norton conectada a la resistencia de carga R_L.

Teorema de Thévenin

En la práctica suele ocurrir que un elemento particular de un circuito sea variable (generalmente se denomina carga) mientras que los demás elementos permanecen fijos. Cada vez que la carga cambia, el circuito entero tiene que volver a analizarse de nuevo. El teorema de Thévenin proporciona una técnica mediante la cual la parte fija del circuito se reemplaza por un circuito equivalente y así se hace más fácil el análisis del efecto del elemento variable en el circuito. Este teorema fue desarrollado en 1883 por el ingeniero de telégrafos francés M. Leon Thévenin.

De acuerdo con el teorema de Thévenin, el circuito lineal de la figura 4.2a) puede reemplazarse por el de la figura 4.2b). (La carga en la figura 4.2 puede ser un solo resistor u otro circuito.) El circuito a la izquierda de las terminales a-b en la figura 4.2b) se conoce como circuito equivalente de Thévenin.

Figura 4.2.- a) Circuito original. b) Circuito equivalente de Thévenin.

En general, el teorema puede usarse para desarrollar lo siguiente:

Analizar redes con fuentes que no están en serie o en paralelo.

Reducir el número de componentes requeridos para establecer las mismas características en las terminales de salida.

Investigar el efecto de cambiar un componente particular en el comportamiento de una red sin tener que analizarla toda después del cambio.

El teorema de Thévenin establece que un circuito lineal de dos terminales puede reemplazarse por un circuito equivalente que consta de una fuente de tensión V_Th(en algunas bibliografías se maneja el símbolo E_Th) en serie con un resistor R_Th, donde V_Th es la tensión de circuito abierto en las terminales y R_Th es la entrada o resistencia equivalente en las terminales cuando las fuentes independientes se apagan.

Los pasos para encontrar el circuito equivalente de Thévenin por el primer método son los siguientes:

1.- Quite la parte de la red donde se encuentra el circuito equivalente de Thévenin (en la Figura 4.2a vendría a ser la parte de la carga).

2.- Marque las terminales de la red restante de dos terminales (Figura 4.3).

Figura 4.3.- Representación de las terminales marcadas al quitar la carga del circuito (recuerde que la carga puede ser una resistencia u otro circuito).

3.- Calcular R_Th. Para calcular R_Thtenemos dos casos

Caso 1: Si la red no tiene fuentes dependientes, se apagan todas las fuentes independientes, las fuentes de tensión se representan como cortocircuito y las fuentes de corriente como circuitos abiertos. En este caso R_Th es la resistencia de entrada que aparece entre las terminales a y b, como se muestra en la figura 4.4.

Figura 4.4.- Calculo de R_Th para fuentes independientes.

Caso 2: Si la red tiene fuentes dependientes, se apagan todas las fuentes independientes. Como en el caso de la superposición, las fuentes dependientes no se desactivan, porque son controladas por las variables del circuito. Se aplica una fuente de tensión V₀ en las terminales a y b y se determina la corriente resultante i₀. Así, R_Th= V₀/i₀, como se señala en la figura 4.5a). Alternativamente, puede insertarse una fuente de corriente I₀ en las terminales a-b, como se muestra en la figura 4.5b), y hallar la tensión entre las terminales V₀. De nuevo, R_Th=V₀/i₀. Los dos métodos dan el mismo resultado, sin embargo debe advertirse que es preferente colocar una fuente de corriente cuando la resistencia esta en paralelo y una fuente de tensión cuando la resistencia se encuentra en serie. En ambos debe suponerse un valor de V₀=1 V o i₀=1 A.

Figura 4.5.- Determinación de R_Th cuando el circuito tiene fuentes dependientes.

4.- Calcular V_Th. Para calcular V_Th se deben regresar primero todas las fuentes a su posición original y determinar el voltaje de circuito abierto entre las terminales marcadas (Figura 4.6).

Figura 4.6.- Calculo de V_Th.

5.- Trace el circuito equivalente de Thévenin con la parte del circuito que previamente se quitó reemplazado entre las terminales del circuito equivalente (Figura 4.7).

Figura 4.7.- Circuito equivalente de Thévenin conectado a la carga.

Ahora considere un circuito lineal con una carga R_L (Figura 4.8a). La corriente I_L a través de la carga y la tensión V_L en sus terminales se determinan con facilidad una vez que se obtiene el equivalente de Thévenin del circuito en las terminales de la carga, como se muestra en la figura 4.8b).

Figura 4.8.- Circuito con una carga: a) Circuito original. b) equivalente de Thévenin.

De aquí tenemos que

Ejemplo 4.1.- Determine el circuito equivalente de Thévenin del área sombreada de la red en la figura 4.9. Luego determine la corriente a través de R_L con valores de 2 Ω, 10 Ω y 100 Ω.

Figura 4.9.- Circuito del ejemplo 4.1.

Primero se quita temporalmente R_L del circuito y se definen las dos terminales a y b (Figura 4.10)

Figura 4.10.- Circuito sin el resistor R_L y las terminales marcadas.

Ahora re reemplazara la fuente de voltaje E₁ por un cortocircuito (Figura 4.11).

Figura 4.11.- Circuito con la fuente de tensión en cortocircuito.

Una vez con el circuito de la figura 4.11 se calcula la R_Th

Ahora se enciende de nuevo la fuente de voltaje (Figura 4.12) y se calcula E_Th, nótese que el E_Thes igual al voltaje que se encuentra en el resistor de 6 Ω.

Figura 4.12.-Circuito con la fuente de tensión encendida.

Aplicando la regla del divisor del voltaje se tiene

Ahora se redibuja el circuito, conectando el circuito equivalente de Thévenin con la R_Lquitada al inicio del análisis (Figura 4.13).

Figura 4.13.- Circuito equivalente de Thévenin.

Usando la formula

Tenemos que para

R_L= 2Ω

R_L= 10Ω

R_L= 100Ω

Ejemplo 4.2.- Halle el equivalente de Thévenin del circuito de la figura 4.14 en las terminales a-b.

Figura 4.14.- Circuito del ejemplo 4.2.

Como ya se mencionó la fuente independiente es la única que se apaga y se agrega una fuente de tensión o corriente, dependiendo del caso, en este se aplicara una fuente de corriente (Figura 4.15).

Figura 4.15.-Circuito con la fuente de corriente apagada y con la fuente de tensión de 1 V agregada.

Aplicando las LTK tenemos para la malla 1 del circuito de la figura 4.15 tenemos

Aplicando las LTK para la malla 2 y malla 3 tenemos que

Malla 2

Malla 3

Pero

Por lo tanto

Sustituyendo el valor de i₁ en las ecuaciones 2 y 3 y resolviendo para i₃ tenemos que

Pero vemos que i₀ va en sentido contrario a i₃, por lo que el valor para i₀es de 1/6 A

Ahora tenemos el circuito de la figura 4.16

Figura 4.16.- Circuito para calcular el VTh

Aplicando las LTK tenemos que

Malla 1

Malla 2

Malla 3

Pero tenemos que

Igualando las ecuaciones 2 y 3 tenemos que

Sustituyendo el valor de i₁ en las ecuaciones 3 y 4, y resolviendo para i₂ tenemos que

Así tenemos que

Ahora dibujamos el circuito equivalente de Thévenin (Figura 4.17).

Figura 4.17.- Circuito equivalente de Thévenin.

Teorema de Norton

En 1926 E. L. Norton, ingeniero estadounidense de Bell Telephone Laboratories, propuso un teorema similar al de Thévenin.

El teorema de Norton establece que un circuito lineal de dos terminales puede reemplazarse por un circuito equivalente que consta de una fuente de corriente I_N en paralelo con un resistor R_N, donde I_N es la corriente de cortocircuito a través de las terminales y R_N es la resistencia de entrada o resistencia equivalente en las terminales cuando las fuentes independientes están desactivadas.

Como se ve el Teorema de Norton parece más una aplicación del teorema de Thévenin. De hecho cabe mencionar que la R_Th=R_N. De igual manera para el teorema de Norton las fuentes dependientes e independientes se tratan igual que en el teorema de Thévenin.

Para encontrar la corriente de Norton I_N, se determina la corriente de cortocircuito que fluye de la terminal “a” a la “b” en los dos circuitos de la figura 4.18. Es evidente que la corriente de cortocircuito de la figura 4.18b) es I_N. Ésta debe ser igual a la corriente de cortocircuito de la terminal “a” a la “b” de la figura 4.18a), ya que ambos circuitos son equivalentes.

Figura 4.18.- a) Circuito origina, b) Circuito equivalente de Norton.

Se tiene entonces que

como se ilustra en la figura 4.19.

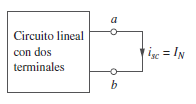Figura 4.19.-Calculo de la corriente de Norton.

La fórmula para el cálculo de i_sc es

Donde podemos apreciar aun de manera más clara la relación entre el teorema de Thévenin y Norton.

Puesto que V_Th, I_N y R_Th se relacionan de acuerdo con dicha ecuación, para determinar el circuito equivalente de Thévenin o de Norton se requiere hallar:

La tensión de circuito abierto v_oc entre las terminales a y b.
La corriente de cortocircuito i_sc por las terminales a y b.
La resistencia equivalente o de entrada R_en en las terminales a y b cuando todas las fuentes independientes están apagadas.

Se pueden calcular dos de las tres siguiendo los mismos pasos que en el teorema de Thévenin y emplearlas para obtener la tercera aplicando la ley de Ohm.

Asimismo, como

las pruebas en circuito abierto y en cortocircuito son suficientes para hallar cualquier equivalente de Thévenin o Norton de un circuito que contenga al menos una fuente independiente. De igual manera una vez que se tiene el circuito equivalente de alguna de las dos formas basta con aplicar una transformación de fuente para hallar el circuito equivalente opuesto (Figura 4.20).

Figura 4.20.- Conversión entre circuitos equivalentes de Thévenin y Norton.

Ejemplo 4.3.- Determine el circuito equivalente de Norton para la red del área sombreada en la figura 4.21.

Figura 4.21.- Circuito del ejemplo 1.

Primero se quita la parte del circuito que corresponde a al resistor R_L, posteriormente se marcan las terminales (Figura 4.22), posteriormente se pone en cortocircuito la fuente de tensión (Figura 4.23)

Figura 4.22.-Circuito sin el resistor R_Ly con las terminales marcadas.

Figura 4.23.- Circuito con la fuente de tensión apagada y puesta en cortocircuito.

Una vez con el circuito de esta forma se calcula la R_N

Ahora se lleva acabo el cortocircuito entre las terminales a y b. Note que la conexión de cortocircuito entre las terminales a y b está en paralelo con R₂ y elimina su efecto. Por consiguiente, I_N es la misma a través de R₁, y el voltaje total de la batería aparece a través de R₁ puesto que

Así que

Reescribimos ahora el circuito equivalente de Norton (Figura 4.24).

Figura 4.24.- Representación del circuito equivalente de Norton conectado al resistor R_L.

Aplicando una transformación de fuente es posible encontrar el circuito equivalente de Thévenin para el mismo circuito (Figura 4.25).

Figura 4.25.- Conversión del circuito equivalente de Norton al de Thévenin.

Ejemplo 4.4.- Halle la resistencia y la intensidad de Norton en las terminales a-b del circuito de la figura 4.26.

Figura 4.26.- Circuito del ejemplo 4.4.

Primero se calcula la R_Th, para eso se apaga la fuente de tensión, así mismo como vemos que tenemos una fuente dependiente en el circuito agregamos una fuente de corriente de 1 A y se redibuja el circuito (Figura 4.27).

Figura 4.27.- Circuito con la fuente de tensión apagada y con la fuente de corriente de 1 A agregada.

Ahora sacamos la resistencia equivalente entre las resistencias de 6 Ω y 3 Ω

Ahora con esta resistencia equivalente redibujamos el circuito (Figura 4.28) y aplicamos el análisis de mallas.

Figura 4.28.- Circuito del ejemplo 2 con la fuente de tensión apagada y la resistencia equivalente.

En este caso solo consideramos una malla, la cual está suministrando 1 A al circuito, por lo que tenemos

Ahora calcularemos la corriente en la fuente dependiente sustituyendo el valor de v₀

Como se ve en la figura 4.28, la corriente de 1 A se divide entre la fuente dependiente y la resistencia de 2 Ω, sabemos que en los elementos conectados en paralelo la intensidad de corriente que entra se divide entre los elementos y sale del mismo valor, por lo que podemos calcular fácilmente que la corriente que circula por la resistencia de 2 Ω es igual a 1/2 A, por lo que podemos calcular el voltaje en dicha resistencia y con ello el voltaje en v_abaplicando las LTK

Con esto calculamos la resistencia de Thévenin o Norton

Para calcular la intensidad de Norton, encendemos la fuente de tensión que habíamos apagado y hacemos un cortocircuito entre las terminales a y b como se muestra en el circuito (Figura 4.29).

Figura 4.29.- Aplicación de la técnica del cortocircuito en las terminales a y b.

Ahora se hará un análisis nodal, se considerara que en el nodo B es aquel donde se encuentra v₀, por lo tanto V_B=v₀ y en el cual están entrando dos corrientes y salen otras dos

Pero el valor de V_A=18 V

Ahora aplicaremos un segundo análisis nodal, en este caso lo haremos en el nodo que está donde está la terminal a, en este caso tendremos dos corrientes que salen y una que entra

Sustituyendo el valor de v₀

Ejemplo 4.5.- Determine el circuito equivalente de Thévenin de la figura 4.30.

Figura 4.30.- Circuito del ejemplo 4.5.

Vemos que en el circuito abierto solo existe un nodo, por lo que calculamos el voltaje en v₁, aplicando un análisis nodal tenemos

Despejando v₁ tenemos que

El cual sería nuestro V_Th.

El paso siguiente consiste en poner en cortocircuito los terminales y calcular la corriente de cortocircuito resultante (Figura 4.31).

Figura 4.31.- Aplicación del cortocircuito a las terminales a y b.

Para obtener la corriente i_sc primero se calcula el voltaje en v₂ aplicando un análisis nodal

Despejando v₂ tenemos que

Aplicando la ley de Ohm tenemos que

Ahora ya podemos calcular la R_Th

Finalmente dibujamos el circuito equiválete de Thévenin (Figura 4.32).

Figura 4.32.- Circuito equivalente de Thévenin.

Como se ve podemos aplicar el método del cortocircuito que se emplea en el cálculo del circuito equivalente de Norton, sin la necesidad de usar el método antes usado para el cálculo del circuito equivalente de Thévenin, con lo que queda en claro aún más la relación entre estos dos teoremas.

Videos explicativos