1.- Linealidad y superposición

Linealidad

La linealidad es la propiedad de un elemento que describe una relación lineal entre causa y efecto. Aunque tal propiedad se aplica a muchos elementos de circuitos, en este capítulo se limitará su aplicación a resistores. Esta característica es una combinación de la propiedad de homogeneidad (escalamiento) y la propiedad aditiva.

La propiedad de homogeneidad establece que si la entrada (también llamada excitación) se multiplica por una constante, la salida (también llamada respuesta) se multiplica por la misma constante. En el caso de un resistor, por ejemplo, la ley de Ohm relaciona la entrada i con la salida v.

Si la corriente se incrementa por una constante k, la tensión se incrementa en consecuencia por k; esto es,

La propiedad aditiva establece que la respuesta a una suma de entradas es la suma de las respuestas a cada entrada aplicada por separado. Con base en la relación tensión corriente de un resistor, si

Entonces la aplicación de (i1 + i2) da como resultado:

Se dice que un resistor es un elemento lineal a causa de que la relación tensión corriente satisface las propiedades tanto de homogeneidad como de aditividad. En general, un circuito es lineal si es tanto aditivo como homogéneo. Un circuito lineal consta únicamente de elementos lineales, fuentes lineales dependientes y fuentes lineales independientes.

Un circuito lineal es aquel cuya salida se relaciona linealmente con (o es directamente proporcional a) su entrada.

Para ilustrar el principio de linealidad, considérese el circuito lineal que se muestra en la figura 1.1.

Figura 1.1.- Circuito lineal.

Este circuito lineal no tiene dentro de él fuentes independientes. Es excitado por una fuente de tensión vs, la cual sirve como entrada. El circuito termina con una carga R. Puede tomarse la corriente i a través de R como salida. Supóngase que vs= 10 V da i = 2A. De acuerdo con el principio de linealidad, vs=1 V dará en i =0.2A. Por la misma razón, i = 1mA tiene que deberse a vs = 5mV.

Ejemplo 1.1.-Suponga que i0=1A y aplique el principio de la linealidad para hallar el valor real de i0 en el circuito

Figura 1.2.- Circuito del ejemplo 1.1

Solución

Para este ejemplo tenemos que i0 =1A entonces V1 = (3+5) i0=8V e I1=V1 / 4=2A por lo tanto aplicamos la LCK al nodo 1 da

La aplicación de la LCK al nodo 2 da

Por lo tanto, si, Is = 5A. Esto demuestra que al suponer que I0 = 1 da por resultado Is = 5A la fuente real de corriente de 15A dará I0 = 3A como el valor real. Suponga que V0 = 1V y aplique el principio de la linealidad para calcular el valor real de V0 en el circuito.

Por lo tanto, la respuesta será: 4 VOLTS

Superposición

Si un circuito tiene dos o más fuentes independientes, una forma de determinar el valor de una variable específica es aplicar el análisis nodal o de malla. Otra es determinar la contribución de cada fuente independiente a la variable y después sumarlas. Este último método se conoce como superposición.

La idea de la superposición se basa en la propiedad de la linealidad.

El principio de superposición ayuda a analizar un circuito lineal con más de una fuente independiente, mediante el cálculo de la contribución de cada fuente independiente por separado. Sin embargo, al aplicarlo deben tenerse en cuenta dos cosas:

1.-Las fuentes que son independientes son una por una cuando siempre y cuando estén las fuentes de tensión apagadas. Por lo cual las fuentes de tensión van a tener un valor de 0 V, se dice que están en corto circuito y los valores que tendrán las fuentes de tensión serán igual a 0 A por lo cual donde se encuentra dicha fuente se transformara en un circuito abierto. 

2.-Las fuente que son dependientes no se modifican para nada, ya que tienen variables con las cuales se trabajan en el circuito. 

El análisis de un circuito aplicando la superposición tiene una gran desventaja: muy probablemente puede implicar más trabajo. Si el circuito tiene tres fuentes independientes, quizá deban analizarse tres circuitos más simples, cada uno de los cuales proporciona la contribución debida a la respectiva fuente individual. Sin embargo, la superposición ayuda a reducir un circuito complejo en circuitos más simples mediante el remplazo de fuentes de tensión por cortocircuitos y de fuentes de corriente por circuitos abiertos.

Tenga en cuenta que la superposición se basa en la linealidad. Por esta razón, no es aplicable al efecto sobre la potencia debido a cada fuente, porque la potencia absorbida por un resistor depende del cuadrado de la tensión o de la corriente. De necesitarse el valor de la potencia, primero debe calcularse la corriente (o tensión) a través del elemento aplicando la superposición.

Ejemplo 1.2.- Aplique el teorema de la superposición para hallar v en el circuito que a continuación se muestra.

Figura 1.3.- Circuito del ejemplo 1.2

Solución

Puesto que hay dos fuentes, se tiene:

donde V1 y V2 son las contribuciones de la fuente de tensión de 6 V y a la fuente de corriente de 3 A, respectivamente. Para obtener V1, la fuente de corriente se iguala en cero, como se indica en la figura 1.4.

Figura 1.4.- Circuito para el analisis de V1

La aplicación de la LTK al lazo de esta última figura se tiene:

Para obtener V2, la fuente de tensión se iguala en cero, como se muestra en el siguiente circuito (figura 1.5).

Figura 1.5.- Circuito para el analisis de V2

Al aplicar el divisor de corriente:

Por lo tanto, el valor de v es igual a 10 volts.

Video explicativo

Problemas de practica

Problema 1.1.-Use la linealidad y suponga que I0 =1mA para calcular la corriente correcta I0 en el circuito de la figura 1.6.

Figura 1.6.- Circuito del ejercicio 1.1

Tome en cuenta que I = 6mA

Respuesta= 3mA

Problema 1.2.-Calcule V0 en el circuito de la figura 1.7 usando el método de superposición.

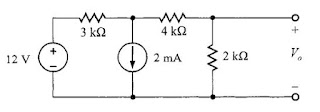Figura 1.7.- Circuito del ejercicio 1.2

Respuesta= 4/3 V